10.3 An Information Processing Perspective on Problem-Solving

The idea of domain-general problem solving by means-ends analysis, subgoals, and working backward was introduced in 1972 by American computer and cognitive scientists Allen Newell and Herbert A. Simon in their book Human Problem Solving. They developed the theory in the late 1950s and 1960s while generating a computer model capable of simulating domain-general human problem solving. For proponents of the Information Processing Perspective on Problem Solving like Newell & Simon (1972), problem solving is thought of as Representation and Search of a Problem Space with a Solution Path.

These Nobel Prize winning scientists called their model the General Problem Solver (GPS). GPS would recursively apply heuristic techniques to solving a given problem and conduct a means-ends analysis after each subproblem or each subgoal was solved to determine whether it was closer to the intended solution or goal. Through this process, GPS could find solutions to mathematical theorems, logical proofs, word problems, and a wide variety of other well-defined problems.

Means-end analysis is a domain-general heuristic, where you identify the “end” (final result or goal) for various subproblems or subgoals (~steps along the way to your goal). Then figure out the “means” (or methods-strategies) you will use to reach those ends or goals.

Another useful heuristic (often combined with Means-end analysis) is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps or subgoals. Students often need to use subgoals to successfully complete a large research project or long paper. The large task becomes less overwhelming when it is broken down into a series of small steps or subgoals.

Examples of the subgoals for writing a research paper often include: students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project.

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. You likely use a working backwards heuristic to plan the events of your day on a regular basis without even realizing it.

One classic “insight” problem where working backwards is useful has come to be called the “Water Lily Problem.”

Often there are obstacles in problem representation, the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely – if indeed the problem can be solved at all. Problem representation would also include determining what information is relevant and what information is irrelevant is the process of problem representation.

For the “Water Lily Problem” the number of water lilies on a lake double each day. How many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is not relevant to the solution, and only serves to distract from the truly crucial information often not used, the fact that the lilies double their coverage each day.

Thus, a working backward domain-general heuristic is often most useful when the end result or goal is clear, but it is unclear how to begin (working forward) to overcome the obstacles to one’s goal(s).

The idea here is that when one doesn’t have much domain knowledge or experience related to a problem that needs solving, one useful approach for both humans and computers is means-end analysis with subgoals and possibly working-backwards, under the conditions outlined above. Two classic examples of means-end analysis with subgoals can be found in the River Crossing Problem and the Tower of Hanoi Problem.

River Crossing Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

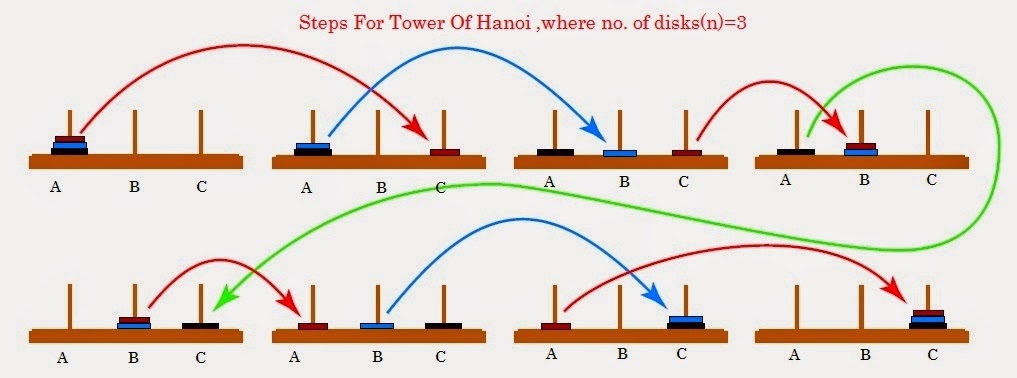
Tower of Hanoi Problem

The Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape.

The initial state of this problem is described by the different sized discs being stacked in order of size (with the smallest on the top) on the first of three pegs (the “start-peg“). The goal state is described by these discs being stacked on the third pegs (the “end-peg“) in exactly the same order (from small at the top to largest at the bottom).

The objective of the puzzle is to move the entire stack to another rod obeying the following rules (or operators):

• Only one disk can be moved at a time from one peg to another one.
• You are only able to move a disc if it is on top of one stack. Each move consists of taking an upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• A disc may Not be placed on top of a smaller disk.

To use Means-End Analysis we usually also create subgoals. One possible way of successfully doing this is for the Tower of Hanoi is the following.

• Moving the discs lying on the biggest one onto the second peg.
• Shifting the biggest disc to the third peg.
• Moving the other ones onto the third peg, too.

You can apply this strategy again and again in order to reduce the problem to the case where you only have to move a single disc – which is then something you are allowed to do.

With 3 disks, the puzzle can be solved in 7 moves: